Liebe Schülerinnen und Schüler,

 

auf dieser Seite habt ihr die Möglichkeit, das Thema „Quadratische Funktionen“ Schritt für Schritt zu bearbeiten, euer Wissen zu überprüfen und eure Kompetenzen gezielt auszubauen.

Wie könnt ihr dabei am besten vorgehen?

• Löst so viele Aufgaben wie möglich eigenständig auf Papier.
• Vergleicht eure Ergebnisse mit den Lösungen (Bild) oder in den Lernvideos.
• Lernt aus euren Fehlern!

 

Viel Erfolg und Freude beim Üben!

Herr Pritzkau

 

Schaue dir dieses Einführungsvideo an ->

Inhalt des Lernvideos

• Einführung in quadratische Funktionen mit der Normalparabel f(x)=x².
• Wertetabelle erstellen und ins Koordinatensystem einzeichnen.
• Typische Parabelform und ihre Darstellung als Graph.
• Veränderungen durch Streckung, Stauchung und Verschiebung.
• Verschiedene Darstellungsformen der Parabel.

 

Aufgabe: Quadratische Funktionen und ihre Darstellung

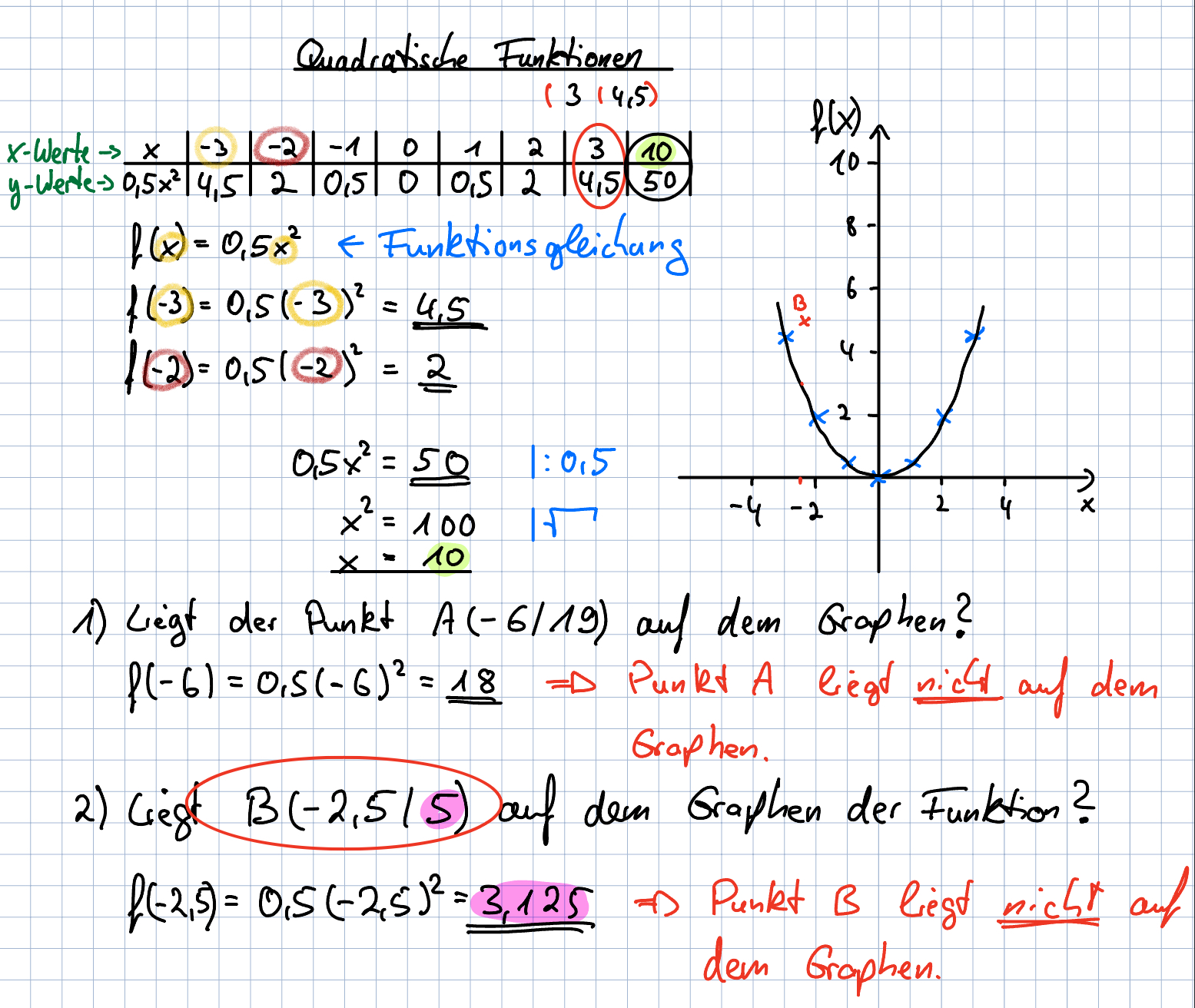
Gegeben ist die Funktion f(x)=0,5x².

1. Berechne die Funktionswerte für die folgenden x-Werte und trage sie in eine Wertetabelle ein (siehe Bild).

2. Zeichne den Graphen der Funktion: Trage die berechneten Punkte in ein Koordinatensystem ein und verbinde sie, um den Verlauf der Parabel darzustellen.

3. Überprüfe, ob bestimmte Punkte auf dem Graphen liegen:

   • a) Liegt der Punkt $A(-6|19)$ auf dem Graphen der Funktion?
   • b) Liegt der Punkt $B(-2,5|5)$ auf dem Graphen der Funktion?

Hinweis: Um die Punkte zu überprüfen, setze den x-Wert des Punktes in die Funktionsgleichung ein und vergleiche das Ergebnis mit dem y-Wert des Punktes.

 

HIER findest du die Lösung zu den Aufgaben --->

Aufgabe: Zeichne folgende Funktion in das Koordinatensystem -->

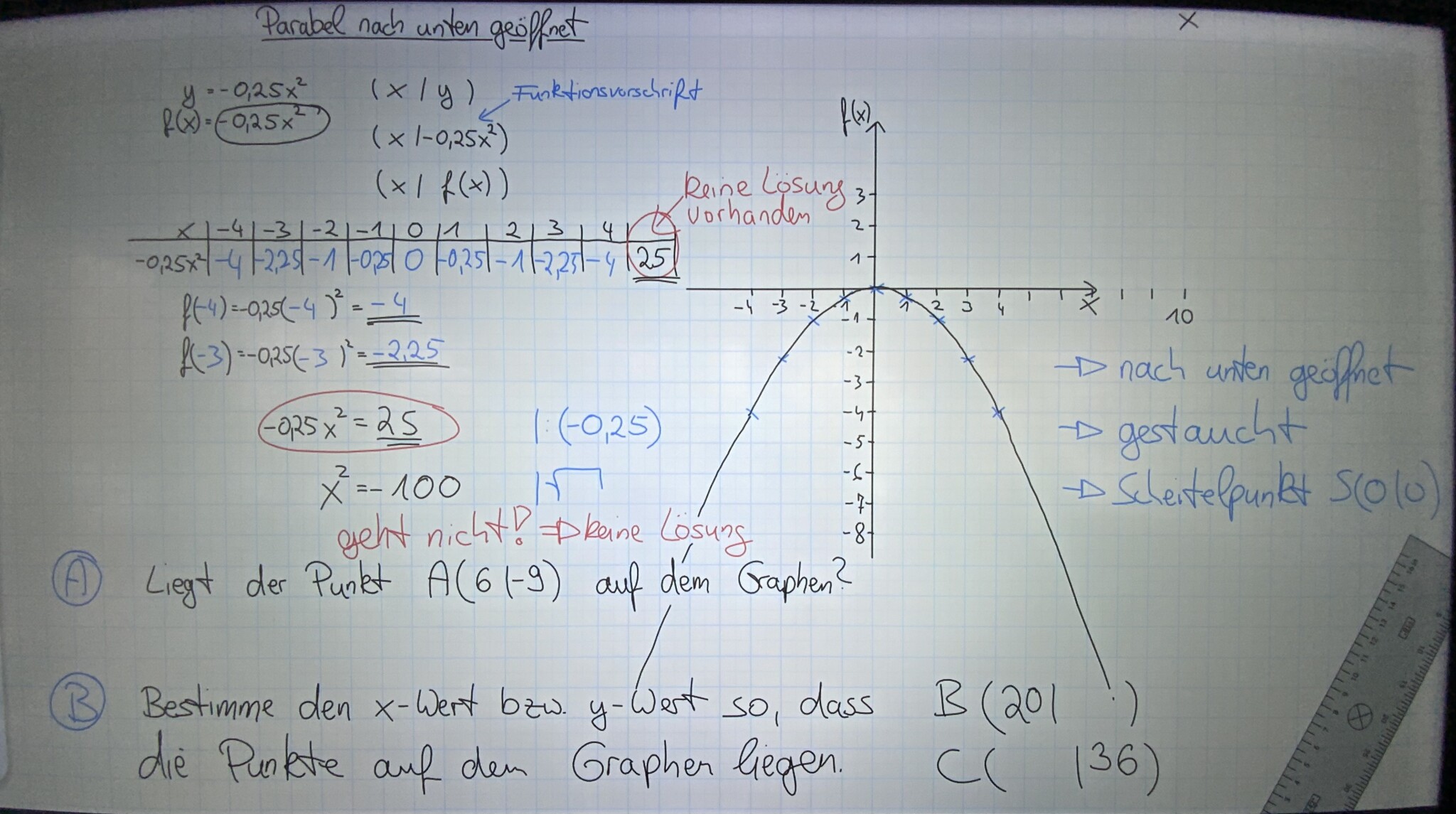
• Erstelle eine Wertetabelle für die Funktion f(x)=−0,5x2f(x) = -0{,}5x^2
• Wähle x-Werte im Bereich von -4 bis 4.
• Berechne für jeden x-Wert den entsprechenden y-Wert.
• Trage die berechneten Punkte (x | y) in ein Koordinatensystem ein.
• Verbinde die Punkte, um den Verlauf der Parabel zu zeichnen.
• Weitere Aufgaben siehe im Bild.

HIER findest du die Lösung zu den Aufgaben --->

Schaue dir dieses Einführungsvideo an ->

Inhalt des Lernvideos

• Erklärung der Grundform der Parabel f(x)=ax2f(x) = ax^2
• Einführung der Verschiebung in y-Richtung durch den Parameter c in der Funktion f(x)=ax2+cf(x) = ax^2 + c
• Positive Werte von $c$: Parabel wird nach oben verschoben.
• Negative Werte von $c$: Parabel wird nach unten verschoben.
• Beispiele zur Veranschaulichung: Zeichnen der Parabeln für verschiedene $c$-Werte.
• Hinweis, dass die Form der Parabel unverändert bleibt – nur die Lage auf der y-Achse ändert sich.
• Zusammenfassung: Verschiebung durch den Parameter c beeinflusst nur die Höhe der Parabel, nicht ihre Breite oder Richtung.