11.-Klasse
Trigonometrische Funktion: Funktionsanalyse (Teil 1)
Bei der trigonometrischen Funktion f(x) = sin(3x) - sin(x) soll nachgewiesen werden, dass sie periodisch mit der Periode 2(pi) ist und zudem...
Zum LernvideoLineare Funktionen: Daniels Junggesellenabschied (Teil 2)
Bei einer Paintballsession belagern vier Personen das Spielfeld. Der Abstand zwischen zwei Spielern soll berechnet und es soll eine Punktpro...
Zum LernvideoLineare Funktionen: Daniels Junggesellenabschied (Teil 1)
Bei einer Paintballsession belagern vier Personen das Spielfeld. Die Spielsituation soll graphisch dargestellt und eine Funktionsgleichung a...
Zum LernvideoLineare Funktionen: Ulrich und der Handytarif (Teil 2)
Zwei Handytarife werden miteinander verglichen. Wann lohnt sich welcher Tarif?...
Zum LernvideoLineare Funktionen: Ulrich und der Handytarif (Teil 1)
Zwei Handytarife werden miteinander verglichen. Wann lohnt sich welcher Tarif?...
Zum LernvideoLineare Funktionen: Funktionsgleichung aus Graphen ablesen
Gegeben sind Funktionsgraphen linearer Funktionen. Aus diesen Graphen sollen die Funktionsvorschriften abgelesen werden....
Zum LernvideoLineare Funktionen: Übungsaufgabe Funktionsgleichung aufstellen
Aus den gegebenen Informationen sollen Lineare Funktionsgleichungen aufgestellt werden....
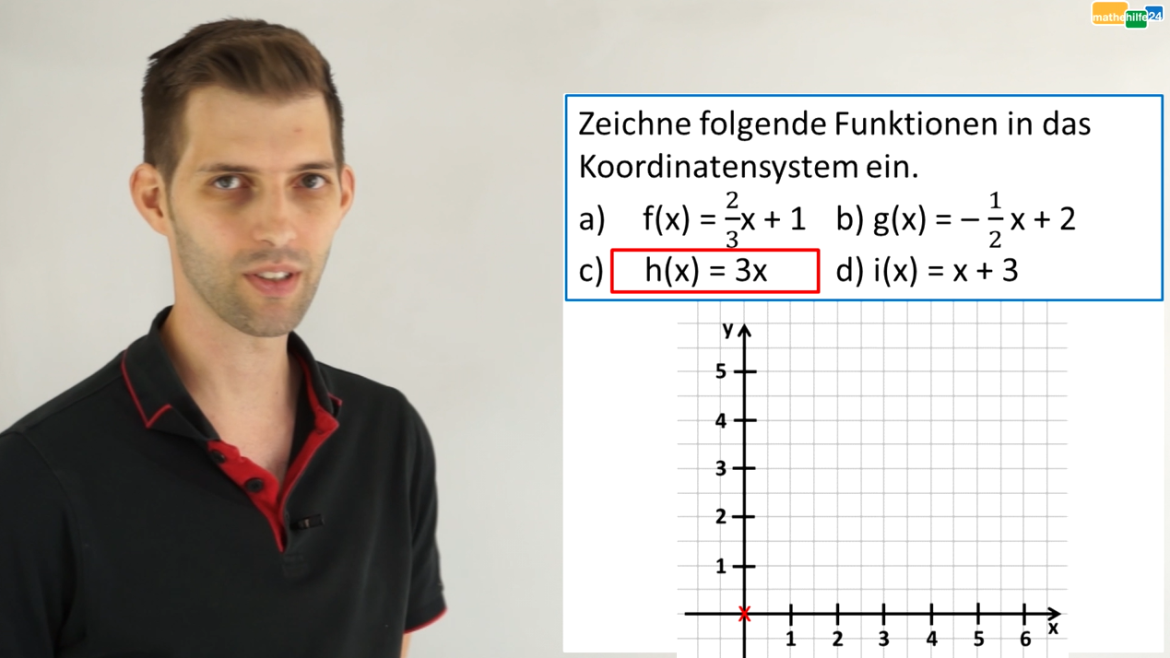
Zum LernvideoLineare Funktionen: Übungsaufgabe Koordinatensystem (Aufgabe c und d)
In diesem Video werden vorgegebene Funktionen in ein Koordinatensystem eingezeichnet....
Zum LernvideoLineare Funktionen: Übungsaufgabe Koordinatensystem (Aufgabe a und b)
In diesem Video werden vorgegebene Funktionen in ein Koordinatensystem eingezeichnet....
Zum LernvideoLineare Funktionen: Das Zylinderfass (oder: Die Regentonne)
Ein Zylinderförmiges Wasserfass ist gegeben. Der Wasserstand steigt gleichmäßig. Mit einer linearen Funktion sollen Wasserstände und Zei...
Zum LernvideoLineare Funktionen: Koordinatenwert bestimmen (Aufgabe b)
Eine Funktionsvorschrift ist gegeben. Außerdem eine Koordinate eines Punktes. Zu finden ist die zweite Koordinate des Punktes....
Zum LernvideoLineare Funktionen: Koordinatenwert bestimmen (Aufgabe a)
Eine Funktionsvorschrift ist gegeben. Außerdem eine Koordinate eines Punktes. Zu finden ist die zweite Koordinate des Punktes....
Zum Lernvideo










LETZTE KOMMENTARE