11.-Klasse
Gerade graphisch bestimmen – Ü4
Aus einem Graphen lesen wir relativ einfach alles raus, was wir benötigen, um die Funktionsgleichung aufzustellen. Hier eine weitere Übung...
Zum LernvideoGerade graphisch bestimmen – Ü3
Aus einem Graphen lesen wir relativ einfach alles raus, was wir benötigen, um die Funktionsgleichung aufzustellen,....
Zum LernvideoGerade graphisch bestimmen – Ü2
In vielen Fällen sind y-Achsenabschnitt und Steigung aus einem Graphen relativ einfach abzulesen bzw. daraus zu bestimmen. In diesem Video ...
Zum LernvideoGeradengleichung graphisch bestimmen – Ü1
Aus einem gegebenen Graphen möchten wir die Funktion bestimmen. Dazu nutzen wir das Steigungsdreieck und lesen den y-Achsenabschnitt direkt...
Zum LernvideoSteigung m bestimmen – Übung
Bei der graphischen Bestimmung der Geradengleichung von linearen Funktionen hilft uns vor allem als Zwischenschritt das Steigungsdreieck. ...
Zum LernvideoBasic: Steigung m & Schnittpunkt b
DIe Allgemeine Geradengleichung kann auch konkret bestimmt werden, sobald eine Funktion vorliegt. Wie man diese graphisch mit Hilfe eines St...
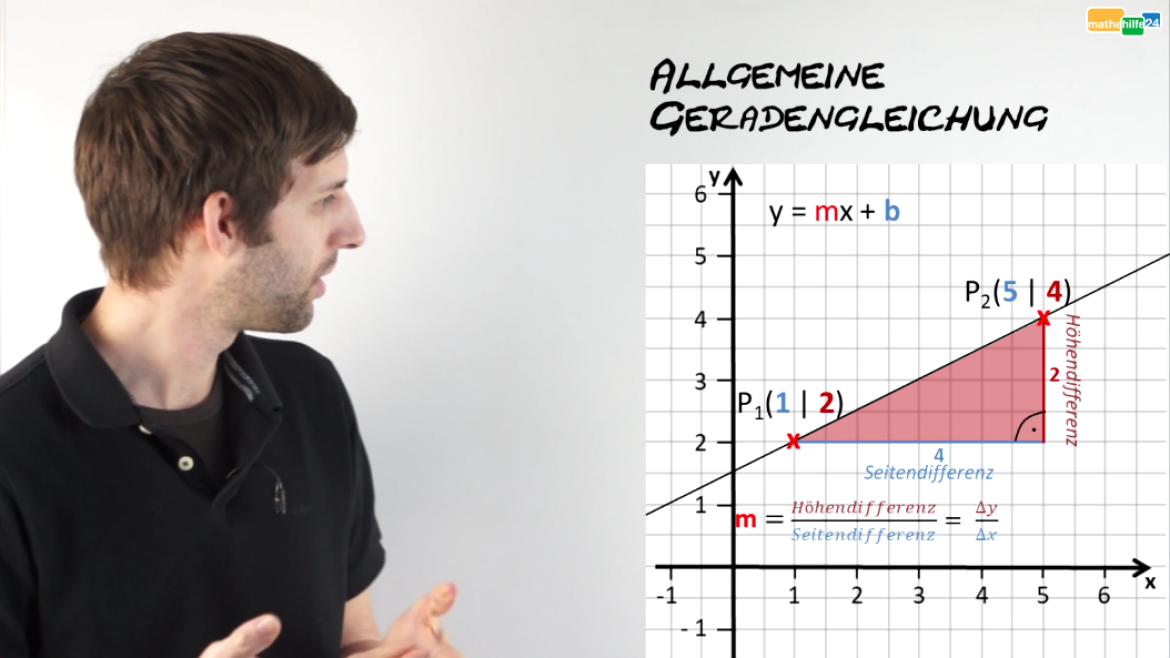
Zum LernvideoAllgemeine Geradengleichung
Funktionen heißen lineare Funktinen, wenn deren Graph eine Gerade ist. Was das konkret bedeutet nd wie eine Geradengleichung entsteht, das ...
Zum LernvideoKurvenuntersuchungen: Extrempunkte
Hier erfährst Du, worauf Du achten musst, wenn Du von einer Funktion die Extrempunkte bestimmen musst....
Zum LernvideoQuadratische Funktion: Die Bogenbrücke (3)
In diesem Video siehst Du, wie Du aus zwei gegebenen Punkten eine lineare Funktion aufstellen kannst....
Zum LernvideoFunktionenschar mit e-Funktion 1.4 Das Handy
Aufgabe: d) Zeigen sie, dass der Modellfunktion fk zufolge die Verkaufszahlen für alle k> 0 ständig sinken, nachdem die maximale Verkau...
Zum LernvideoTrassierung – Rutsche III – Modellierung durch den Graph einer ganzrationalen Funktion
Aufgabe: Entwerfen Sie eine 4m hohe Rutsche, deren Steigung an der steilsten Stelle genau 45° beträgt. In diesem Video w...
Zum LernvideoTrassierung – Rutsche II – Modellierung durch den Graph einer ganzrationalen Funktion
Das seitliche Profil der Rutsche soll durch den Graphen einer ganzrationalen Funktion modelliert werden und durch deren Extrempunkte begrenz...
Zum Lernvideo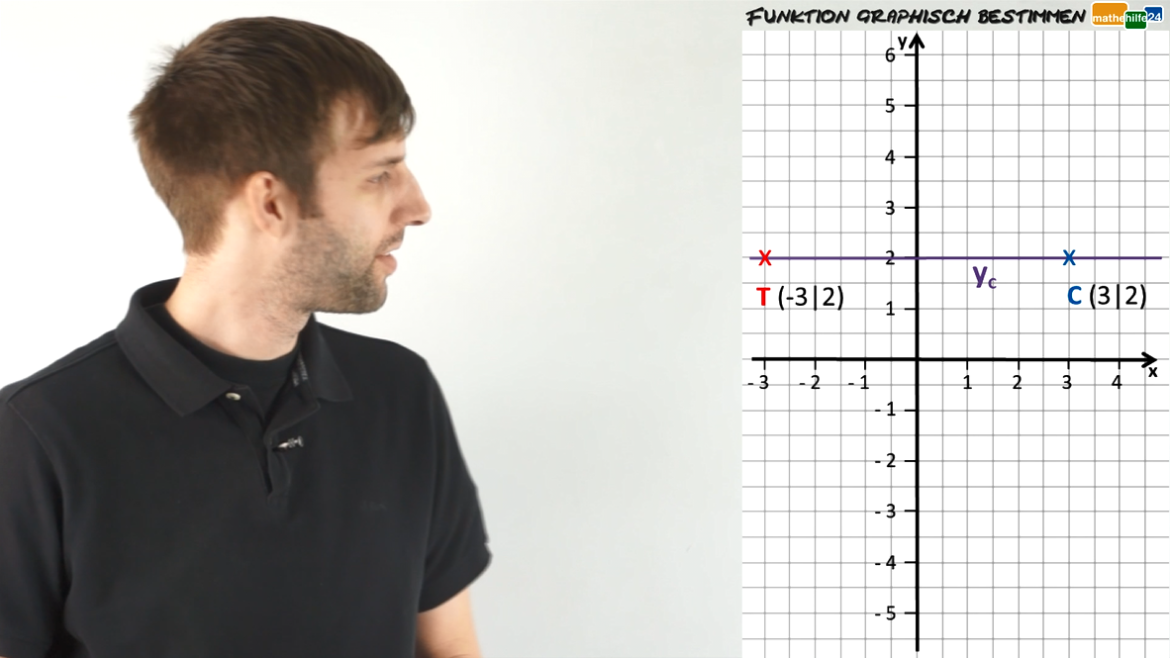






LETZTE KOMMENTARE